Diferença entre paralelogramo e quadrilátero: paralelogramo versus quadrilátero
Paralelogramo vs. Quadrilateral < Quadrilaterais e paralelogramos são polígonos encontrados na geometria euclidiana. O paralelogramo é um caso especial do quadrilátero. Os quadriláteros podem ser planar (2D) ou 3 Dimensões, enquanto os paralelogramos são sempre planos.
Quadrilateral
O quadrilátero é um polígono com quatro lados. Tem quatro vértices, e a soma dos ângulos internos é 3600 (2π rad). Os quadriláteros são classificados em categorias quadrilaterais auto-intersectadas e simples. Os quadrilaterais auto-intersectados têm dois ou mais lados se cruzando, e figuras geométricas menores (como triângulos são formadas dentro do quadrilátero).
Os quadriláteros simples também são divididos em quadriláteres convexos e côncavos. Quadrilaterais côncavos têm lados adjacentes formando ângulos reflexos dentro da figura. Os quadriláteros simples que não possuem ângulos reflexos internamente são quadriláteros convexos. Os quadriláteros convexos sempre podem ter tesselagens.

O paralelogramo pode ser definido como a figura geométrica com quatro lados, com lados opostos paralelos entre si. Mais precisamente, é um quadrilátero com dois pares de lados paralelos. Esta natureza paralela dá muitas características geométricas aos paralelogramos.
Um quadrilátero é um paralelogramo se forem encontradas características geométricas.

• Dois pares de lados opostos são iguais em comprimento. (AB = DC, AD = BC)
• Dois pares de ângulos opostos são iguais em tamanho. ()

• Um par de lados, que se opõem um ao outro, é paralelo e de comprimento igual. (AB = DC & AB∥DC)
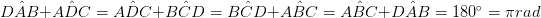
• As diagonais se bispam entre si (AO = OC, BO = OD)
• Cada diagonal divide o quadrilateral em dois triângulos congruentes. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)
Além disso, a soma dos quadrados dos lados é igual à soma dos quadrados das diagonais. Isso às vezes é referido como a
lei de paralelogramo e tem aplicações generalizadas em física e engenharia. (AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2 ) Cada uma das características acima pode ser usada como propriedades, uma vez que se estabelece que o quadrilátero é um paralelogramo.
A área do paralelogramo pode ser calculada pelo produto do comprimento de um lado e da altura ao lado oposto. Portanto, a área do paralelogramo pode ser declarada como
Área de paralelogramo = base × altura =
AB × h A área do paralelogramo é independente da forma do paralelogramo individual. Depende apenas do comprimento da base e da altura perpendicular.

Se os lados de um paralelogramo podem ser representados por dois vetores, a área pode ser obtida pela magnitude do produto vetorial (produto cruzado) dos dois vetores adjacentes.
Se os lados AB e AD forem representados pelos vetores () e (





• A área do paralelogramo é dividida pela metade por qualquer linha que passa pelo ponto médio.
• Qualquer transformação afim não degenerada leva um paralelogramo a outro paralelogramo
• Um paralelogramo tem simetria rotacional de ordem 2
• A soma das distâncias de qualquer ponto interior de um paralelogramo para os lados é independente de a localização do ponto
Qual a diferença entre Paralelogramo e Quadrilateral?
• Os quadriláteros são polígonos com quatro lados (às vezes chamados de tetragons), enquanto o paralelogramo é um tipo especial de quadrilátero.
• Os quadriláteros podem ter seus lados em planos diferentes (no espaço 3d), enquanto todos os lados do paralelogramo estão no mesmo plano (plano / 2dimensional).
• Os ângulos interiores do quadrilátero podem tomar qualquer valor (incluindo ângulos reflexos), de modo que eles somam até 3600. Os paralelogramos só podem ter ângulos obtusos como o tipo máximo de ângulo.
• Quatro lados do quadrilátero podem ter diferentes comprimentos, enquanto os lados opostos do paralelogramo são sempre paralelos entre si e de comprimento igual.
• Qualquer diagonal divide o paralelogramo em dois triângulos congruentes, enquanto os triângulos formados pela diagonal de um quadrilátero geral não são necessariamente congruentes.


