Diferença entre integralidades indefinidas e indefinidas A diferença entre
O cálculo é um ramo importante da matemática, e a diferenciação desempenha um papel crítico no cálculo. O processo inverso da diferenciação é conhecido como integração, e o inverso é conhecido como integral, ou simplesmente, o inverso da diferenciação dá uma integral. Com base nos resultados que produzem, as integrais são divididas em duas classes a saber., integrais definitivas e indefinidas.
Definite Integral
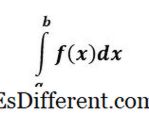
A integral definida de f (x) é um NÚMERO e representa a área sob a curva f (x) de x = a para x = b .
Uma integral definida possui limites superiores e inferiores nas integrais, e é chamado de definitivo porque, no final do problema, temos um número - é uma resposta definitiva.
Indefinido Integral

A integral indefinida de f (x) é uma FUNÇÃO e responde a pergunta: "Qual função quando diferenciada dá f (x) ? "
Com uma integral indefinida, não há limites superiores e inferiores na integral aqui, e o que receberemos é uma resposta que ainda tem x 's e também terá uma constante (geralmente denotado por C ) nele.
Integral indefinido geralmente dá uma solução geral para a equação diferencial.
A integral indeterminada é mais uma forma geral de integração, e pode ser interpretada como a anti-derivada da função considerada.
Suponha que a diferenciação da função F leve a outra função f , e a integração de f fornece a integral. Simbolicamente, isso é escrito como
F (x) = ∫ƒ (x) dx
ou
F = ∫ƒ dx
em que ambos F e ƒ < são funções de x e F é diferenciável. Na forma acima, ele é chamado de Reimann integral e a função resultante acompanha uma constante arbitrária. Uma integral indefinida geralmente produz uma família de funções; portanto, a integral é indefinida.
Os processos integrados e de integração estão no centro da resolução de equações diferenciais. No entanto, ao contrário dos passos de diferenciação, os passos na integração nem sempre seguem uma rotina clara e padrão. Ocasionalmente, vemos que a solução não pode ser expressa explicitamente em termos de função elementar. Nesse caso, a solução analítica é muitas vezes dada sob a forma de uma integral indefinida.
Teorema Fundamental do Cálculo
A integral definida e a integral indefinida estão ligadas pelo Teorema Fundamental do Cálculo como segue: Para calcular uma
integral definida , encontre a integral indefinida > (também conhecido como o anti-derivativo) da função e avalie nos pontos finais x = a e x = b . A diferença entre integrais definitivas e indefinidas será evidente uma vez que avaliamos as integrais para a mesma função. Considere a seguinte integral:
OK. Vamos fazer os dois e ver a diferença.
Para a integração, precisamos adicionar um ao índice que nos leva à seguinte expressão:

Neste ponto de tempo
C
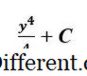
é apenas uma constante para nós. Informações adicionais são necessárias no problema para determinar o valor preciso de C . Vamos avaliar a mesma integral em sua forma definida i. e., com os limites superior e inferior incluídos. Graficamente falando, agora estamos calculando a área sob a curva
f (x) = y

3 entre y = 2 e y = 3 >. O primeiro passo nesta avaliação é o mesmo que a avaliação integral indefinida. A única diferença é que, desta vez, não adicionamos a constante C .
A expressão neste caso é a seguinte: Esta é a vez leva a: Essencialmente, substituímos 3 e depois 2 na expressão e obtivemos a diferença entre eles.
Este é o valor definido em oposição ao uso de constante

C

anterior.
Vamos explorar o fator constante (em relação à integral indefinida) com mais detalhes. Se o diferencial de y
3
for 3y 2 , então ∫ 3y 2
dy = y 3 No entanto, 3y 2
pode ser o diferencial de muitas expressões, algumas das quais incluem y 3 -5 , > y 3 +7 , etc … Isso implica que a reversão não é única uma vez que a constante não é reconhecida durante a operação. Então, em geral, 3y 2 é o diferencial de
y 3 + C onde C é qualquer constante. Aliás, C é conhecido como 'constante de integração' . Nós escrevemos isso como: ∫ 3y 2
. dx = y
3 + C As técnicas de integração para uma integral indefinida, como a pesquisa de tabela ou a integração do Risch, podem adicionar novas descontinuidades durante o processo de integração. Estas novas descontinuidades aparecem porque os anti-derivados podem exigir a introdução de logaritmos complexos. Logaritmos complexos têm uma descontinuidade de salto quando o argumento cruza o eixo real negativo, e os algoritmos de integração às vezes não conseguem encontrar uma representação onde esses saltos cancelam.




