Diferença entre Derivativo e Diferencial

Derivado vs Diferencial

No cálculo diferencial, derivado e diferencial de uma função estão intimamente relacionados, mas têm significados muito diferentes e usado para representar dois importantes objetos matemáticos relacionados a funções diferenciáveis.

O que é derivado?

Derivada de uma função mede a taxa em que o valor da função muda à medida que sua entrada muda. Nas funções de múltiplas variáveis, a alteração no valor da função depende da direção da alteração dos valores das variáveis independentes. Portanto, em tais casos, uma direção específica é escolhida e a função é diferenciada nessa direção particular. Esse derivado é chamado derivado direcional. Derivados parciais são um tipo especial de derivados direcionais.

Derivada de uma função com valor vetorial f pode ser definida como o limite

onde ele existe finitamente. Como mencionado anteriormente, isso nos dá a taxa de aumento da função f ao longo da direção do vetor u. No caso de uma função de valor único, isso reduz a definição bem conhecida da derivada,

Por exemplo,

é em todo o lado diferenciável, e a derivada é igual ao limite,

, que é igual a

. Os derivados de funções como

existem em todos os lugares. Eles são respectivamente iguais às funções

Isto é conhecido como a primeira derivada. Normalmente, a primeira derivada da função f é denotada por f ⁽¹⁾ . Agora, usando esta notação, é possível definir derivadas de ordem superior.

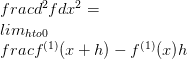
é a derivada direcional de segunda ordem e denotando a n ^th derivada por f ⁽ⁿ⁾ para cada n,

, define a n ^th derivada.

O que é diferencial?

O diferencial de uma função representa a mudança na função em relação às mudanças na variável ou variáveis independentes. Na notação usual, para uma determinada função f de uma única variável x, o diferencial total da ordem 1 df é dado por

. Isto significa que, para uma mudança infinitesimal em x (ou seja, d x), haverá f ⁽¹⁾ (x <) d x alteração em f. Usando limites pode-se terminar com esta definição da seguinte maneira. Assuma Δ

x é a alteração em x em um ponto arbitrário x e Δ f é a alteração correspondente na função f. Pode-se mostrar que Δ f = f (1) ⁽ x) Δ x + ε, onde ε é o erro. Agora, o limite Δ x → 0 Δ ^{f /} Δ _{x =} f (1) ( ^x ) (usando a definição de derivada anteriormente indicada) e, portanto, Δ x → 0 ε / ^Δ x = 0.Portanto, é possível concluir que, Δ _{x → 0} ε = 0. Agora, denotando Δ x → 0 Δ f como d f e Δ x → 0 Δ x como d x a definição do diferencial é rigorosamente obtida. Por exemplo, o diferencial da função é.

No caso de funções de duas ou mais variáveis, o diferencial total de uma função é definido como a soma dos diferenciais nas direções de cada uma das variáveis independentes. Matematicamente, pode ser declarado como

Qual a diferença entre derivativo e diferencial?

• Derivada refere-se a uma taxa de alteração de uma função, enquanto o diferencial se refere à mudança real da função, quando a variável independente é submetida a alteração.

• A derivada é dada por

, mas o diferencial é dado por

Diferença entre Derivativo e Diferencial

Recomendado