Diferença entre Parabola e Hiperbola
Parabola vs Hyperbola
Kepler descreveu as órbitas dos planetas como elipses que foram posteriormente modificados por Newton, pois ele mostrou essas órbitas para ser seções cônicas especiais, como a parábola e a hipérbole. Existem muitas semelhanças entre uma parábola e uma hipérbole, mas há diferenças também, pois existem diferentes equações para resolver problemas geométricos envolvendo essas seções cônicas. Para entender melhor as diferenças entre uma parábola e uma hipérbole, precisamos entender essas seções cônicas.
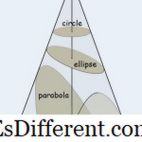
Cortesia da imagem: // cseligman. com
Uma seção é uma superfície ou o contorno dessa superfície formada pelo corte de uma figura sólida com um plano. Se a figura sólida for um cone, a curva resultante é chamada de seção cônica. O tipo e a forma da seção cônica são determinados pelo ângulo de interseção do plano e do eixo do cone. Quando o cone é cortado perpendicularmente ao eixo, obtemos uma forma circular. Quando cortado em menos de um ângulo reto, mas mais do que o ângulo feito pelo lado do cone resulta em uma elipse. Quando cortado paralelamente ao lado do cone, a curva obtida é uma parábola e quando cortada quase paralelamente ao eixo que ao lado, obtemos uma curva conhecida como hipérbole. Como você pode ver nas figuras, círculos e elipses são curvas fechadas, enquanto as parábolas e as hipérbolas são curvas abertas. No caso de uma parábola, os dois braços eventualmente se tornam paralelos entre si, enquanto que no caso de uma hipérbole não é assim.
Como os círculos e as parábolas são formados cortando um cone em ângulos específicos, todos os círculos são de forma idêntica e todas as parábolas são de forma idêntica. No caso de hipérbolas e elipses, existe uma ampla gama de ângulos entre o plano eo eixo, e é por isso que eles tendem a ter uma ampla gama de formas. As equações dos quatro tipos de seções cônicas são as seguintes.
Circle-x 2 + y 2 = 1
Elipse - x 2 / a 2 + y 2 / b 2 = 1 Parabola-
2 = 4ax Hyperbola- x
2 / a 2 - y 2 / b 2 = 1



